Middelbare scholen verdienen betere prognoses
In steeds meer organisaties worden adviezen tegenwoordig gebaseerd op data. Datagedreven werken raakt hierdoor steeds meer ingeburgerd. Onderwijsinstellingen daarentegen hebben door hun non-profitstatus een andere missie en traditie. Dat wil echter niet zeggen dat zij niet kunnen profiteren van onderwijsinnovatie, een datagedreven strategie en data science. Integendeel. In deze blog tonen we aan de hand van concrete praktijkvoorbeelden aan dat een zogenoemd leerlingvoorspelsysteem een welkome aanvulling kan zijn op de al bestaande leerlingvolgsystemen.
Hoeveel data heb je nodig?
Het goede nieuws is dat een middelbare school heel veel data verzamelt tijdens het verblijf van een leerling. Denk hierbij aan de eindtoets en het advies van de basisschool, repetitie- en rapportcijfers, gegevens over wel of niet zittenblijven, verzuimcijfers, wel of geen diploma enzovoorts. Al deze data kunnen scholen gebruiken als hefboom om adviezen te geven die goed onderbouwd zijn, adviezen die bovendien het vertrouwen genieten van leerlingen en ouders. Maar hoe doe je dat? Het antwoord is simpel: binnen de context van een continu verbeterende, datagedreven organisatie.
De keuzestress slaat toe
Tijdens het verblijf van een leerling op de middelbare school zijn er regelmatig cruciale keuzemomenten. Voorbeelden van beslissingen die over en met de leerling en ouders gemaakt moeten worden zijn: wat is het advies na de brugklas havo of vwo? Is het advies aan het einde van klas 3 wiskunde A of wiskunde B? In hoeverre is het gekozen profiel een goede keuze met het oog op de arbeidsmarkt, baanzekerheid et cetera. Deze adviezen moeten naast de inschatting van de docenten zoveel mogelijk gebaseerd zijn op feiten, op harde data. En bij voorkeur op zoveel mogelijk data. Dit komt de onderbouwing van en het vertrouwen in het advies alleen maar ten goede.
Datagedreven werken in het onderwijs
Datagedreven werken in het algemeen is het sturen op basis van (onbewerkte) feiten en data om een werk- en verbeteractie op gang te brengen. Hierbij vinden transformaties plaats: je gaat data verzamelen en transformeren tot informatie. Interpretatie van de informatie leidt vervolgens tot inzichten zoals trends en patronen waaruit verbeterinitiatieven ontstaan.
Datagedreven werken in het onderwijs is werken op basis van feiten uit de school die verzameld worden in de vorm van data (repetitiecijfers et cetera). Deze worden geanalyseerd en omgezet naar informatie (zoals samenvattende scores). Samen met onderwijskennis en de juiste interpretaties ontstaan bruikbare inzichten. Op basis van deze inzichten wordt een zo geïnformeerd mogelijk besluit genomen over de gewenste verbeteringen. (zie figuur 1).
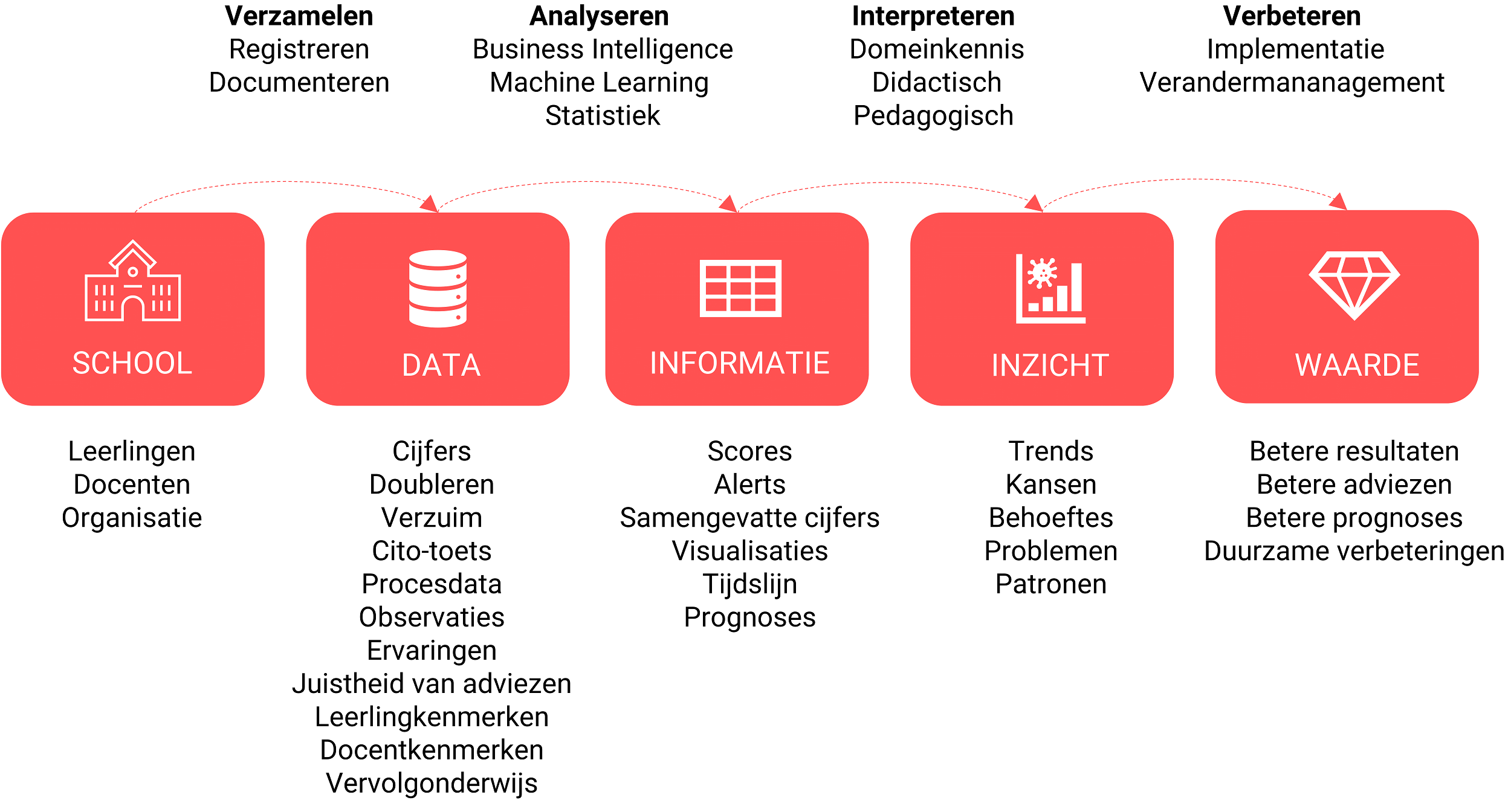
Figuur 1: Het informatieverwerkingsproces van een middelbare school
Het doel is om dagelijks meer inzicht en kennis te verwerven en meer gefundeerde beslissingen te nemen op basis van betrouwbare data. Je gaat niet meer alleen sturen op basis van het onderbuikgevoel of meningen. Graag verwijs ik naar Andries Bottema’s whitepaper ‘De datagedreven onderwijsinstelling‘ voor een uitgebreide beschrijving en handleiding voor datagedreven werken in het onderwijs.
PDCA cyclus onderwijs
Nauw verbonden met datagedreven werken is het continu verbeteren van je processen en zo uit te groeien tot een volwassen, intelligente, datagedreven onderwijsorganisatie. Dat kan door te werken volgens de PDCA cyclus (Plan-Do-Check-Act), ontwikkeld door dr. William Edwards Deming.
Datagedreven werken in het onderwijs houdt in dat je dagelijks meer inzicht en kennis gaat verwerven en meer gefundeerde beslissingen gaat nemen op basis van betrouwbare data.
PDCA is een krachtige, beproefde methode om processen te verbeteren en te komen tot een lerende, continu verbeterende school. De methode beschrijft vier activiteiten die op alle verbeteringen in onderwijsorganisaties van toepassing zijn. De vier activiteiten zorgen uiteindelijk voor een betere kwaliteit. Het cyclische karakter garandeert dat de kwaliteitsverbetering continu onder de aandacht blijft.
Vier activiteiten
De vier activiteiten in de kwaliteitscirkel van Deming zijn:
- PLAN: Kijk naar de huidige werkzaamheden en ontwerp een plan voor de verbetering van deze werkzaamheden. Stel voor deze verbetering doelstellingen vast.
- DO: Voer de geplande verbetering uit in een gecontroleerde proefopstelling.
- CHECK: Meet het resultaat van de verbetering en vergelijk deze met de oorspronkelijke situatie en toets deze aan de vastgestelde doelstellingen.
- ACT: Stel bij aan de hand van de gevonden resultaten bij CHECK.
Na de ACT stap begint de cyclus opnieuw met een aangepast PLAN en zo verder.
De opleiding Data Science  Tijdens onze 'Master of Data Science' op HBO+ niveau maak je in tien compacte dagen grondig kennis met Data Science, AI, Business Intelligence, Predictive Analytics, textmining en Big Data. Je leert hoe je een business case kan opstelllen (voor het onderwijs), je gaat de valkuilen herkennen, en je leert om te gaan met privacy & ethiek. Maar vooral krijg je handvatten hoe je data science in jouw school / instelling kan organiseren en managen. Tot slot krijg je diepgaand inzicht in de succesfactoren.
Tijdens onze 'Master of Data Science' op HBO+ niveau maak je in tien compacte dagen grondig kennis met Data Science, AI, Business Intelligence, Predictive Analytics, textmining en Big Data. Je leert hoe je een business case kan opstelllen (voor het onderwijs), je gaat de valkuilen herkennen, en je leert om te gaan met privacy & ethiek. Maar vooral krijg je handvatten hoe je data science in jouw school / instelling kan organiseren en managen. Tot slot krijg je diepgaand inzicht in de succesfactoren.
Twee praktijkvoorbeelden van onderwijsinnovatie
We illustreren datagedreven werken volgens de PDCA-methode aan de hand van twee voorbeelden uit de praktijk, toegespitst op de 3e klas middelbare school en het vak wiskunde.
1. Advies wiskunde A of wiskunde B
a. Kun je een voorspelmodel maken voor de kans op succes wiskunde B in de 4e klas?
b. Kun je het keuzeproces wiskunde-A of wiskunde-B verbeteren?
2. Wiskunderesultaten in de 4e klas
a. Kun je een voorspelmodel maken voor het eindrapportcijfer in de 4e klas?
b. Kun je de leerprestaties verbeteren door aanpassingen in didactiek, onderwijsmethode, et cetera
Advies: wiskunde A of B?
VWO-leerlingen moeten in klas 3 de keuze maken tussen wiskunde A en B. Of C als de school dat aanbiedt. We beperken ons in dit voorbeeld echter tot A en B. Die keuze is onder meer afhankelijk van de vervolgstudiekeus van de leerling (mogelijk is wi-B daar een voorwaarde of denkt de leerling dat), maar ook van de capaciteiten, motivatie et cetera van de leerling. En dan zijn er nog de ouders die denken dat wi-B beter en/of verstandiger is en daardoor soms extreme druk uitoefenen op leerlingen om hiervoor te kiezen.
De praktijk leert dat er een voorkeur is voor wi-B en dat houdt een risico in. Een leerling die ten onrechte wi-B heeft gekozen en terug moet naar wi-A omdat het niet lukt (“overstapper”), moet vervolgens veel wi-A stof inhalen en dat blijkt in de praktijk lastig te zijn. Kortom, een goed advies met goede onderbouwing kan helpen om de juiste keuze te maken.
Wat we eigenlijk willen is gedurende klas 3 regelmatig een voorspelling doen van de kans op succes met wi-B. Op die manier krijgen docent en leerling continu feedback over hoe het er per leerling voorstaat en kan er tijdig worden bijgestuurd. Aan het eind van klas 3 moet de keuze wi-A of wi-B definitief zijn, maar het is nuttig om gaandeweg het schooljaar al een trend te zien.
Voorspelling 1: wat is de kans op succes met wiskunde B
Stel je wilt het aantal overstappers reduceren. Je gaat dan op zoek naar mogelijke voorspellers in beschikbare data. Voor welke leerlingen was wi-B achteraf gebleken een goede keus? Wat zijn de cijfers en kenmerken (zoals verzuim, het onregelmatig maken huiswerk, et cetera) van leerlingen die beter wi-A hadden kunnen kiezen. Met deze informatie maak je een voorspelmodel om het advies beter te onderbouwen
Supervised learning in het onderwijs
Laten we de hiervoor genoemde adviesvraag wi-A of wi-B verder uitwerken. Het model dat we gaan beschrijven valt in het vakgebied data science en wel binnen de categorie machine learning. Specifiek gaat het om zogenoemde supervised learning, dat wil zeggen het model wordt getraind op basis van feedback die het ontvangt.
In ons voorbeeld willen we de kans op overstappen voorspellen. Om machine learning modellen te trainen gebruiken we historische data: van leerlingen die in klas 3 wi-B gekozen hebben en klas 4 hebben afgerond verzamelen we dan:
- rapport- en repetitiecijfers wiskunde van de klassen 1, 2 en 3
- leerlinggegevens over verzuim et cetera.
- de overstapgegevens (ja of nee) uit klas 4, dat wil zeggen of de leerling terug naar wi-A moest omdat wi-B niet lukte.
Het model krijgt dus steeds inputdata (cijfers, verzuim et cetera) met de bijbehorende output (overstappen ja of nee), waarbij het leeralgoritme zoekt naar relevante verbanden en/of voorspellers. Als het model getraind is – de stappen die nodig zijn om te komen tot een goede set voorspellers laten we hier achterwege – kan het in het volgende schooljaar worden gebruikt om nieuwe leerlingen te adviseren.
In een praktijkcase, uitgevoerd op een gymnasium, bleek dat de kans op overstappen van wi B naar wi A in klas 4 goed kon worden voorspeld met de eindrapportcijfers wiskunde klas 1 en 2, en de cijfers van negen repetities in klas 3. Deze negen repetities gaan dus over onderwerpen die relevant zijn voor wiskunde B.
Het eerste voorspelmoment is na de 1e repetitie in klas 3 (tijdstip t3 in onderstaande grafiek). Op dat moment zijn er nog maar drie voorspellers bekend (eindrapport klas 1, eindrapport klas 2 en 1e repetitie klas 3). We kunnen echter al wel een voorspelling doen op grond van deze cijfers, ook al is de betrouwbaarheid nog niet zo hoog. Naarmate meer cijfers bekend zijn, zal de voorspelling tijdens het schooljaar nauwkeuriger worden.
Omdat het aantal voorspellers per voorspelmoment (t3 t/m t11) toeneemt, maken we in totaal negen modellen:
- Model 1 (tijdstip t3) voorspelt de kans op succes wi-B na de 1e repetitie in klas 3, voorspellers zijn dan: eindrapport klas 1, eindrapport klas 2 en 1e repetitie klas 3.
- Model 2 (tijdstip t4) voorspelt de kans op succes wi-B na de 2e repetitie in klas 3, voorspellers zijn dan: eindrapport klas 1, eindrapport klas 2, 1e repetitie klas 3 en 2e repetitie klas 3.
- enzovoorts tot en met model 9
Discriminantanalyse in het onderwijs
In onderstaande grafiek (figuur 2) zijn de voorspellingen van een fictieve leerling geplot. Het algoritme dat is gebruikt is discriminantanalyse, een algoritme dat goed kan discrimineren tussen verschillende categorieën (in dit geval wi-A en wi-B).
De voorspelling wordt aangegeven met 1 (groen, advies wi-B) of 0 (rood, advies wi-A). De eerste voorspelling in klas 3 is groen (wi-B) en de bijbehorende probabiliteit (een maat voor de betrouwbaarheid van de voorspelling) is .75. Daarna verandert het advies naar wi-A, met als uitzondering de voorspelling na repetitie 4. De probabiliteit gaat gedurende het jaar richting 0 voor wi-B: de kans op succes met wi-B is laag.
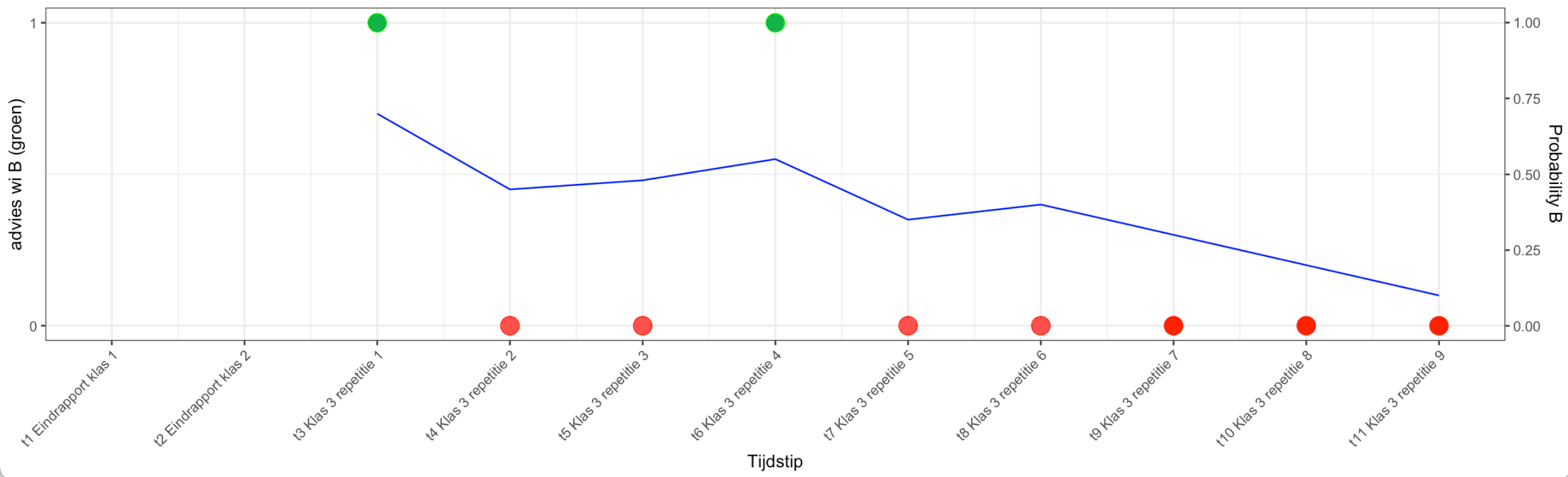
Figuur 2: Plot van een fictieve leerling op basis van een discriminantanalyse
Wat we hier dus zien, is dat de kans op wi-B succes vanaf tijdstip t4 (2e repetitie in klas 3) 50-50 is. De docent kan deze informatie goed gebruiken om dit met de leerling te bespreken.
NB: het gaat hier niet om een trend in een tijdreeks, maar om voorspellingen gebaseerd op specifieke repetitiecijfers (repetities die dus veel zeggen over de kans op succes met wi-B) en andere kenmerken van de leerling. Bij een tijdreeks is de tijd tussen de meetpunten op de x-as gelijk, in bovenstaande grafiek is dat niet het geval. Elk punt op de x-as geeft hier aan welke voorspellende cijfers er op dat moment bekend zijn.
In tegenstelling tot leerlingvolgsystemen (zoals bijvoorbeeld Magister) hebben we hier dus een leerlingvoorspelsysteem. Terwijl een leerlingvolgsysteem terugblikt, kijken we hier vooruit en doen we voorspellingen die steeds betrouwbaarder worden.
Het PDCA-handboek 'Datacratisch werken' In dit complete PDCA-boek komt het hele spectrum van datacratisch werken aan bod. Dit is een splinternieuwe, veelbelovende manier van werken. De auteur gaat uitgebreid in op de basisprincipes van PDCA, continu verbeteren en leerprocessen in organisaties.Inclusief unieke AI assistent.
In dit complete PDCA-boek komt het hele spectrum van datacratisch werken aan bod. Dit is een splinternieuwe, veelbelovende manier van werken. De auteur gaat uitgebreid in op de basisprincipes van PDCA, continu verbeteren en leerprocessen in organisaties.Inclusief unieke AI assistent.In dit voorbeeld ging het om het “advies wiskunde”, maar een vergelijkbaar model zou je bijvoorbeeld ook kunnen maken om de kans op succes te voorspellen van een te kiezen studieprofiel.
Verbeteren keuzeproces wiskunde A of B
Nu kunnen we de kans op succes voorspellen, maar het is natuurlijk ook belangrijk om te kijken of je het adviesproces zelf nog kan verbeteren. De PDCA aanpak kan daarbij helpen, hieronder volgt een voorbeeld:
- PLAN. Stel het huidige percentage overstappers is 10% en voor het volgende schooljaar wil je dit reduceren naar 5%.
- DO. Je gaat vaker voorlichtingssessies houden over de verschillen tussen wiskunde-A en wiskunde-B, zodat de leerling een beter onderbouwde welbewuste keuze kan maken. Ook geef je gedetailleerd aan voor welke universitaire studies wiskunde-B verplicht is.
- CHECK. Aan het einde van het schooljaar evalueer je het proces voor klas 3: hebben je voorlichtingssessies de leerlingen geholpen? Welke feedback heb je gekregen van de leerlingen? Had het voorspelmodel toegevoegde waarde? Kon je het advies beter onderbouwen? Klopt het advies van het model met je eigen beeld van de leerling?
- ACT. Met de resultaten en feedback breid je je voorlichtingsprogramma uit. Na een jaar (dan weet je of het advies juist was), breid je het voorspelmodel uit met de nieuwe data, zodat het model voor het volgend schooljaar nog beter kan voorspellen.
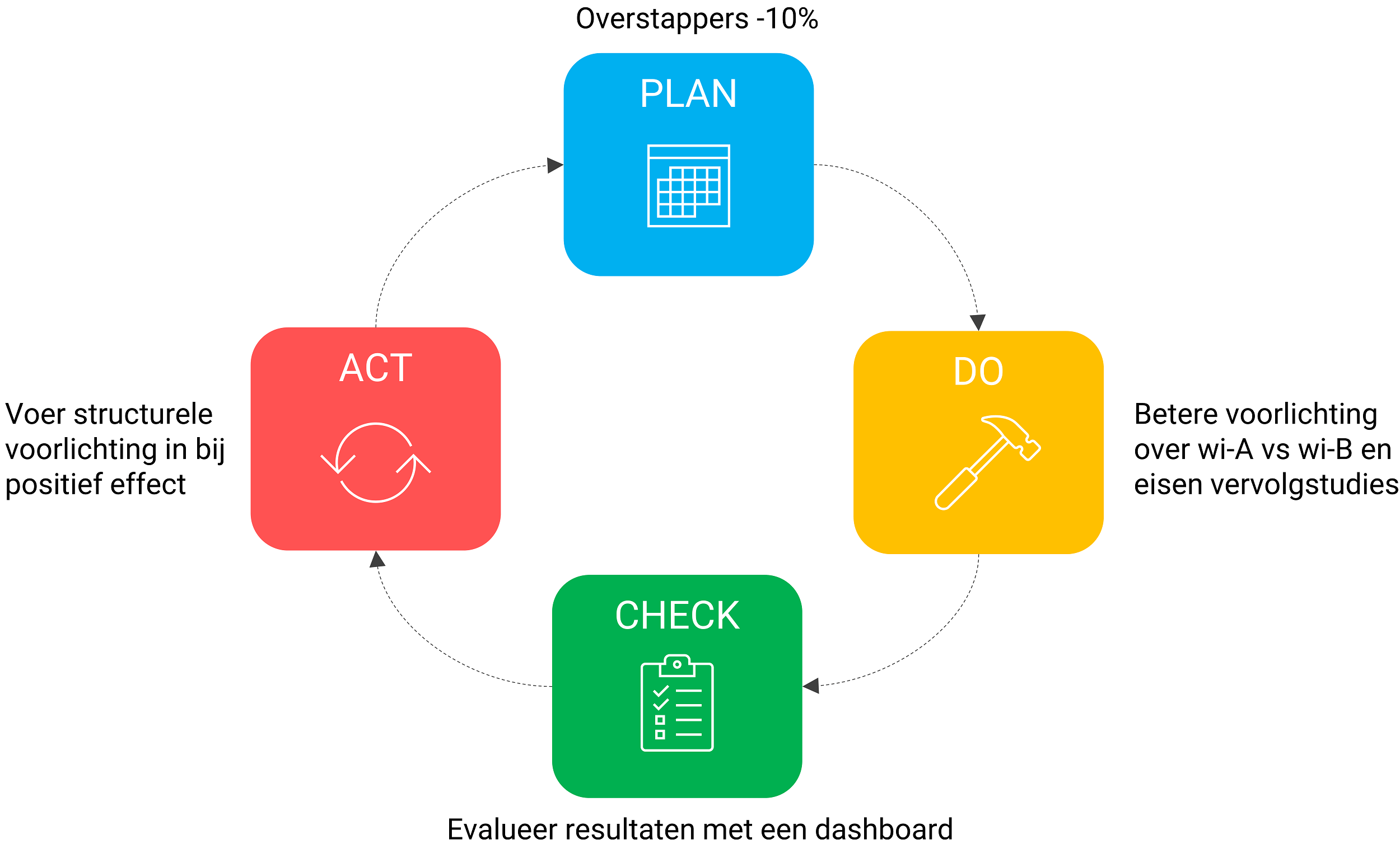
Figuur 3: PDCA-cirkel toegepast op het adviesproces
Na de Act-stap begint de cyclus opnieuw met een aangepast Plan en zo verder. Op deze manier kan er continu verbeterd worden. Een volgende “Do”-actie zou kunnen zijn: het aanbieden van een wiskunde-B test. Als er een goede test is gevonden, kun je de resultaten daarvan ook meenemen in het voorspelmodel.
Voorspelling 2: wat zijn de wiskunderesultaten in de 4e klas?
Afgezien van de keuze wiskunde A of B is het nuttig om tijdens een schooljaar in klas 3 steeds een prognose te kunnen geven van de resultaten in klas 4. Het voorspelmodel dat we hier gekozen hebben is multipele regressie: we voorspellen een numerieke waarde (eindrapportcijfer wiskunde in klas 4) op basis van meerdere voorspellers.
Ook hier weer doen we een voorspelling, steeds op grond van meer data. Uit vooronderzoek kwamen twaalf repetities (t1 t/m t12, klas 1,2 en 3, zie grafiek) naar voren die een voorspellende waarde hebben voor het eindrapportcijfer in klas 4. Elk repetitiecijfer is een separate voorspeller, omdat per repetitie de lesstof anders is. Repetitiecijfers zijn dus veel specifieker dan rapportcijfers.
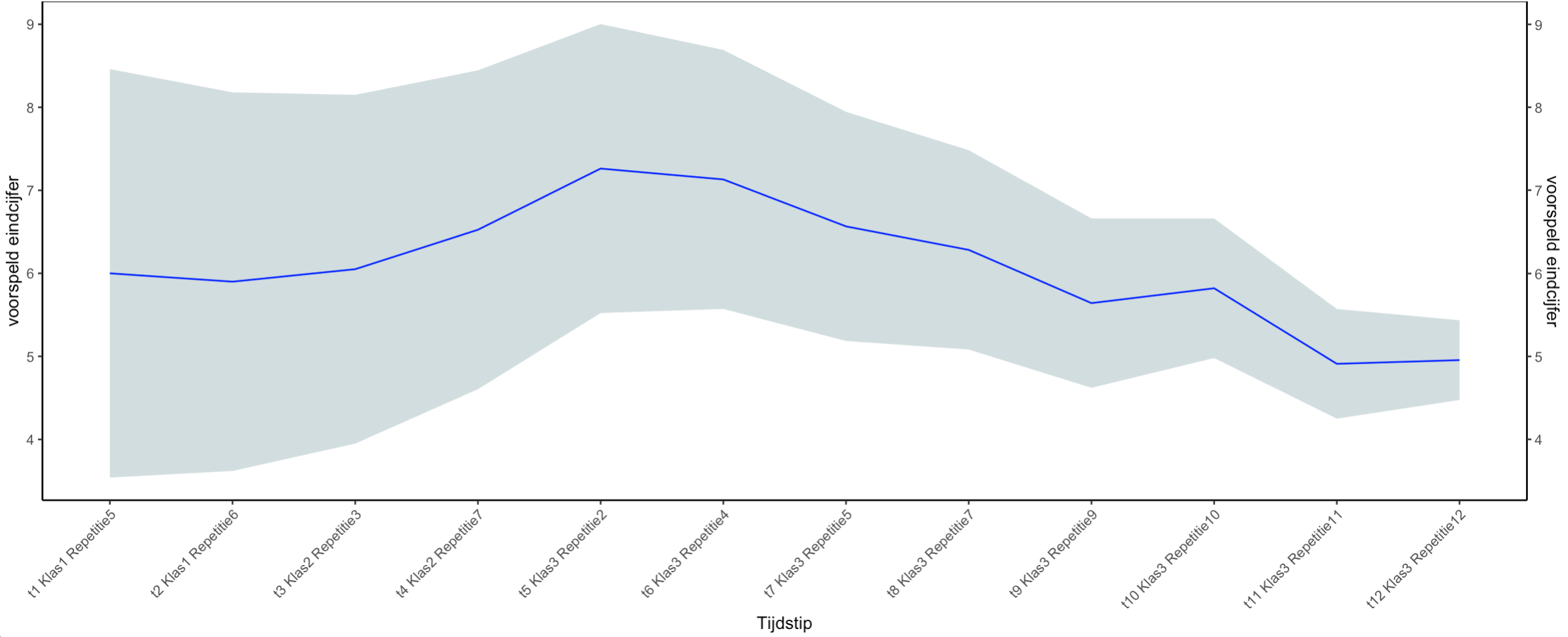
Figuur 4: Voorspelling wiskunderesultaten op basis van multipele regressie
Ook hier neemt het aantal voorspellers in de tijd toe: de voorspelling op tijdstip t5 (begin klas 3) is gebaseerd op 5 voorspellers (repetities 1 en 2 klas, 3 en 7 klas 2 en repetitie 2 klas 3), t6 op 6 voorspellers et cetera. Net als in het wiskundevoorbeeld hebben we hier te maken met een model per voorspellingstijdstip. Ook zaken als verzuim en dergelijke worden als predictor toegevoegd.
De blauwe lijn is het voorspelde eindrapportcijfer, de grijze band geeft het betrouwbaarheidsinterval weer. Uiteraard is de betrouwbaarheid hoger (en het interval kleiner) naarmate de voorspelling dichter bij het moment van overgang naar klas 4 ligt en het voorspellingsmodel gebaseerd is op meer data (t12). We zien een piek op tijdstip t5 (na repetitie 2 in klas 3). Het voorspelde eindrapportcijfer is een 7 met een betrouwbaarheidsinterval tussen een 5 en een 9. Daarna daalt het voorspelde eindrapportcijfer, waarbij de betrouwbaarheid van de voorspelling toeneemt (het interval wordt smaller).
NB net als in het wiskundevoorbeeld gaat het hier niet om een trend in een tijdreeks, maar om voorspellingen gebaseerd op specifieke repetitiecijfers.
Onderwijsinnovatie en het laaghangende fruit
Hoe en waar kun je beginnen met datagedreven werken? Wanneer je in je organisatie op een andere manier wilt gaan werken is het verstandig om met kleine stappen te beginnen, een geschikt project te kiezen, en met een enthousiast team aan de slag te gaan. Een evolutionaire aanpak om met ‘evidence-based’ verbeteren te starten. Laaghangend fruit betekent in deze context dat je een bekend probleem kiest, het proces gaat verbeteren en tegelijkertijd de organisatie daarin betrekt en enthousiast maakt. Veel succes!
Verbeteren wiskunderesultaten
Naast het hiervoor besproken voorspellen van het eindrapportcijfer klas 4 kunnen we gaan onderzoeken of de wiskundecijfers zelf nog verbeterd kunnen worden. De PDCA-onderwijs aanpak kan ook hierbij weer helpen:
- PLAN: Stel het huidige percentage onvoldoendes is 10% en voor het volgende schooljaar wil je dit reduceren naar 5%.
- DO: Je gaat experimenteren met extra SO’s in een parallelklas.
- CHECK: Je vergelijkt de cijfers met behulp van een statistische toets.
- ACT: Bij positieve resultaten voer je de extra SO’s in alle klassen in.
Figuur 5: PDCA-cirkel toegepast op wiskundecijfers
Na de Act-stap begint de cyclus opnieuw met een aangepast Plan en zo verder. Je kunt zo eindeloos experimenteren met oefeningen, projecten, lesduur et cetera. Op deze manier kan er continu verbeterd worden.
Conclusie
Data science kan een belangrijke bijdrage leveren aan het streven van onderwijsorganisaties om meer datagedreven te gaan werken. Met name supervised learning en multipele regressiemodellen bieden een grote voorspellende waarde voor de toekomstige prestaties van leerlingen. Met deze concrete praktijkvoorbeelden hebben we willen illustreren hoe datagedreven werken volgens de PDCA-cyclus een school kan helpen de adviesprocessen continu te verbeteren.
Tot slot
Een betere onderbouwing van schooladviezen op grond van data kan de kwaliteit van die adviezen verhogen en dat is goed voor leerlingen, docenten, scholen en last but not least de gemoedsrust van ouders.